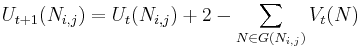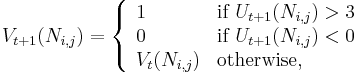Knight's tour
The knight's tour is a mathematical problem involving a knight on a chessboard. The knight is placed on the empty board and, moving according to the rules of chess, must visit each square exactly once. A knight's tour is called a closed tour if the knight ends on a square attacking the square from which it began (so that it may tour the board again immediately with the same path). Otherwise the tour is open. The exact number of open tours is still unknown. Creating a program to solve the knight's tour is a common problem given to computer science students.[1] Variations of the knight's tour problem involve chessboards of different sizes than the usual 8 × 8, as well as irregular (non-rectangular) boards.
Contents |
Theory
The knight's tour problem is an instance of the more general Hamiltonian path problem in graph theory. The problem of finding a closed knight's tour is similarly an instance of the Hamiltonian cycle problem. Note, however, that unlike the general Hamiltonian path problem, the knight's tour problem can be solved in linear time.[2]
History
The earliest known references to the Knight's Tour problem date back to the 9th century AD. The pattern of a knight's tour on a half-board has been presented in verse form (as a literary constraint) in the highly stylized Sanskrit poem Kavyalankara[3] written by the 9th century Indian poet Rudrata, which discusses the art of poetry, especially with relation to theater (Natyashastra). As was often the practice in ornate Sanskrit poetry, the syllabic patterns of this poem elucidate a completely different motif, in this case an open knight's tour on a half-chessboard.
One of the first mathematicians to investigate the knight's tour was Leonhard Euler. The first procedure for completing the Knight's Tour was Warnsdorff's rule, first described in 1823 by H. C. von Warnsdorff.
In the 20th century, the Oulipo group of writers used it among many others. The most notable example is the 10 × 10 Knight's Tour which sets the order of the chapters in Georges Perec's novel Life: A User's Manual. The sixth game of the 2010 World Chess Championship between Viswanathan Anand and Veselin Topalov saw Anand making 13 consecutive knight moves (albeit using both knights) -– online commentors jested that Anand was trying to solve the Knight's Tour problem during the game.
Closed tours
On an 8 × 8 board, there are exactly 26,534,728,821,064 directed closed tours (i.e. two tours along the same path that travel in opposite directions are counted separately, as are rotations and reflections).[4][5][6] The number of undirected closed tours is half this number, since every tour can be traced in reverse. There are 9,862 undirected closed tours on a 6 × 6 board.[7] No closed tours exist for smaller square boards besides the trivial case 1 × 1 (this is a corollary of the following theorem).
Schwenk's Theorem
For any m × n board with m less than or equal to n, a closed knight's tour is always possible unless one or more of these three conditions are met:
- m and n are both odd; m and n are not both 1
- m = 1, 2, or 4; m and n are not both 1
- m = 3 and n = 4, 6, or 8.
Condition 1
One can show that condition 1 prohibits closed tours by a simple argument based on parity and coloring. For the standard black-and-white coloring of the chessboard, the knight must move either from a black square to a white square or from a white square to a black square. Thus in a closed tour the knight must visit the same number of white squares as black squares, and the number of squares visited in total must therefore be even. But if m and n are both odd, the total number of squares is odd. (For example, in a 5 × 5 checkerboard there are 13 of one color and 12 of the other.) Therefore closed tours do not exist. Open tours may still exist (with the exception of the trivial case 1 × 1).
Condition 2
Condition 2 states that when the shorter side is of length 1, 2, or 4, no closed tour is possible.
When m = 1 or 2, no closed tour is possible because the knight would not be able to reach every square (once again, with the exception of the trivial case 1 × 1). It can be shown that a 4 × n board cannot have a closed tour either, by using a coloring argument.
Start by assuming that a 4 × n board has a closed knight's tour. Letbe the set of all squares that would be black and
all the squares that would be white, if they were colored according to the alternating black-and-white checkerboard scheme. Consider the figure at right. Define
to be the set of green squares and
as the set of red squares. There are an equal number of red squares as green squares. Note that from a square in
the knight must next jump to a square in
. And since the knight must visit every square once, when the knight is on a square in
it must move to a square in
next (otherwise the knight will need to travel to two squares in
later).
If we follow the hypothetical knight's tour, we will find a contradiction.
- The first square the knight goes to will be a square of
 and
and  . If it is not, we switch the definitions of
. If it is not, we switch the definitions of 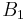 and
and 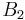 so that it is true.
so that it is true. - The second square must be an element of the sets
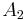 and
and 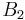 .
. - The third square must be an element of
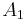 and
and 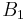 .
. - The fourth square must be an element of the sets
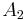 and
and 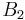 .
. - And so on.
It follows that set 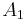 has the same elements as set
has the same elements as set 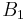 , and set
, and set 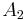 has the same elements as set
has the same elements as set 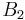 . But this is obviously not true, as the red and green pattern shown above is not the same as a checkerboard pattern; the set of red squares is not the same as the set of black squares (or white, for that matter).
. But this is obviously not true, as the red and green pattern shown above is not the same as a checkerboard pattern; the set of red squares is not the same as the set of black squares (or white, for that matter).
So our above assumption was false and there are no closed knight's tours for any 4 × n board, for any n.
Condition 3
Condition 3 may be proved using casework. Attempting to construct a closed knight's tour on a 3 by 4, 3 by 6, or 3 by 8 will lead to definite failure. 3 by n boards with n even and greater than 8 can be shown to have closed tours by induction (a repeating pattern).
All other cases
Simply proving the above three conditions does not prove the theorem. It is still required to prove that all rectangular boards that do not fall in one of the above three categories have closed knight's tours.[8]
Computer algorithms
Algorithms other than the simple brute-force search to find knight's tour solutions are discussed below. It is important to note that an exhaustive brute force approach (one which iterates through all possible move sequences) should never be applied to the Knight's Tour problem (except for very small board sizes). For a regular 8x8 chess board, there are approximately 4×1051 possible move sequences,[9] and it would take an unfathomable amount of time to iterate through such a large number of moves.
Divide and conquer solutions
By dividing the board into smaller pieces, constructing tours on each piece, and patching the pieces together, one can construct tours on most rectangular boards in polynomial time.[10][11]
Neural network solutions
The Knight's Tour problem also lends itself to being solved by a neural network implementation.[12] The network is set up such that every legal knight's move is represented by a neuron, and each neuron is initialized randomly to be either "active" or "inactive" (output of 1 or 0), with 1 implying that the neuron is part of the final solution. Each neuron also has a state function (described below) which is initialized to 0.
When the network is allowed to run, each neuron can change its state and output based on the states and outputs of its neighbors (adjacent knight's moves) according to the following transition rules:
where  represents discrete intervals of time,
represents discrete intervals of time, 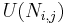 is the state of the neuron connecting square
is the state of the neuron connecting square  to square
to square  ,
, 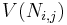 is the output of the neuron from
is the output of the neuron from  to
to  , and
, and 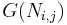 is the set of neighbors of the neuron.
is the set of neighbors of the neuron.
Although divergent cases are possible, the network should eventually converge, which occurs when no neuron changes its state from time  to
to 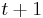 . When the network converges, a solution is found. The solution found by the network will be either a knight's tour, or a series of two or more independent knight's tours within the same board.
. When the network converges, a solution is found. The solution found by the network will be either a knight's tour, or a series of two or more independent knight's tours within the same board.
Warnsdorff's rule
Warnsdorff's rule is a heuristic method for finding a knight's tour. Briefly, one moves the knight according to the following rule: always proceed to the square from which the knight will have the fewest onward moves. When calculating the number of onward moves for each candidate square, of course, we do not count moves that revisit any square already visited. It is, of course, possible to have two or more choices for which the number of onward moves is equal; there are various methods for breaking such ties, including one devised by Pohl [13] and another by Squirrel and Cull.[14]
This rule may also more generally be applied to any graph. In graph-theoretic terms, each move is made to the adjacent vertex with the least degree. Although the Hamiltonian path problem is NP-hard in general, on many graphs that occur in practice this heuristic is able to successfully locate a solution in linear time.[13] The knight's tour is a special case.[15]
The heuristic was first described in "Des Rösselsprungs einfachste und allgemeinste Lösung" by H. C. von Warnsdorff in 1823.[15]
Procedure for Applying the Rule
Warnsdorff’s rule can be applied for any initial position of the knight on the board. All the possible squares which may be reached in one move from this position are located, and the number of moves that the knight would be able to make from each of these squares is found.[16] Then, the rule dictates that the knight move to the square that has the least number of possible following moves. The process is then repeated until each square has been visited.[15][17]
Some definitions:
- A position Q is accessible from a position P if P can move to Q by a single knight's move, and Q has not yet been visited.
- The accessibility of a position P is the number of positions accessible from P.
Procedure:
- set P to be a random initial position on the board
- mark the board at P with the move number "1"
- for each move number from 2 to the number of squares on the board:
- let S be the set of positions accessible from the input position
- set P to be the position in S with minimum accessibility (breaking ties by any preferred method, such as selecting at random)
- mark the board at P with the current move number
- return the marked board – each square will be marked with the move number on which it is visited.
See also
Notes
- ^ H. M. Deitel, P. J. Deitel. "Java How To Program Fifth Edition." Prentice Hall, Upper Saddle River, New Jersey, pp. 326–328. 2003.
- ^ Conrad, A.; Hindrichs, T.; Morsy, H. & Wegener, I. (1994). "Solution of the Knight's Hamiltonian Path Problem on Chessboards". Discrete Applied Mathematics 50 (2): 125–134. doi:10.1016/0166-218X(92)00170-Q.
- ^ Satyadev, Chaudhary. Kavyalankara of Rudrata (Sanskrit Text, with Hindi translation);. Delhi: Parimal Sanskrit Series No. 30.
- ^ Martin Loebbing; Ingo Wegener (1996). "The Number of Knight's Tours Equals 33,439,123,484,294 — Counting with Binary Decision Diagrams". The Electronic Journal of Combinatorics 3 (1): R5. http://www.combinatorics.org/Volume_3/Abstracts/v3i1r5.html. Remark: The authors later admitted that the announced number is incorrect. According to McKay's report, the correct number is 13,267,364,410,532 and this number is repeated in Wegener's 2000 book.
- ^ Brendan McKay (1997). "Knight's Tours on an 8x8 Chessboard". Technical Report TR-CS-97-03 (Department of Computer Science, Australian National University). http://www.combinatorics.org/Volume_3/Comments/v3i1r5.01.ps.
- ^ Wegener, I. (2000). Branching Programs and Binary Decision Diagrams. Society for Industrial & Applied Mathematics. ISBN 0-898-71458-3. http://books.google.com/?id=-DZjVz9E4f8C&pg=PA369&dq=532.
- ^ Weisstein, Eric W., "Knight's Tour" from MathWorld.
- ^ Watkins, John J. (2004). Across the Board: the Mathematics of Chessboard Problems. Princeton University Press. ISBN 0691115036.
- ^ "Enumerating the Knight's Tour". http://www.josiahland.com/?p=781.
- ^ Cull, P.; DeCurtins, J. (June 1978). "Knight's Tour Revisited". Fibonacci Quarterly 16: 276–285.
- ^ Parberry, Ian (1997). "An Efficient Algorithms for the Knight's Tour Problem". Discrete Applied Mathematics 73: 251–260. doi:10.1016/S0166-218X(96)00010-8. http://larc.unt.edu/ian/pubs/algoknight.pdf.
- ^ Y. Takefuji, K. C. Lee. "Neural network computing for knight's tour problems." Neurocomputing, 4(5):249–254, 1992.
- ^ a b Pohl, Ira (July 1967). "A method for finding Hamilton paths and Knight's tours". Communications of the ACM 10 (7): 446–449. doi:10.1145/363427.363463. http://portal.acm.org/citation.cfm?id=363463.
- ^ Squirrel, Douglas; Cull, P. (1996). "A Warnsdorff-Rule Algorithm for Knight's Tours on Square Boards". https://github.com/douglassquirrel/warnsdorff/blob/master/5_Squirrel96.pdf?raw=true. Retrieved 2011-08-21.
- ^ a b c Alwan, Karla; Waters, K. (1992). "Finding Re-entrant Knight's Tours on N-by-M Boards" (PDF). ACM Southeast Regional Conference. New York, New York: ACM. pp. 377–382. doi:10.1145/503720.503806. http://portal.acm.org/citation.cfm?id=503806. Retrieved 2008-10-28.
- ^ Törnberg, Gunno (1999). "Warnsdorff's rule". http://web.telia.com/~u85905224/knight/eWarnsd.htm. Retrieved 2008-09-25.
- ^ Cancela, Hector; Mordecki, Ernesto (2006-08-31) (PDF). Counting Knight’s Tours through the Randomized Warnsdorff Rule. http://www.cmat.edu.uy/~mordecki/articles/warnsdorff.pdf. Retrieved 2008-10-18.
External links
- Richard W. Henderson, Eugene Roger Apodaca A Knight of Egodeth: Zen Raptured Quietude, 240 Solutions to the Knights Tour in form of Game Book
- Warnsdorff's Rule and its efficiency from Warnsdorff's Rule Web Page
- Velucchi, Mario. "The ultimate Knight's Tour page of Links". http://www.velucchi.it/mathchess/knight.htm.
- Thomasson, Dan. "The knight's tour". http://www.borderschess.org/KnightTour.htm.
- Knight's tour notes
- (sequence A001230 in OEIS)
- Preprint of Pohl's paper (freely accessible)
- SilverKnight - online knight's tour game
- Knightfall - online version of the game as presented by the Riddler.
- warnsdorff.com - Page devoted to Warnsdorff's Rule
Implementations
- The Knight's Tour by Jay Warendorff, Wolfram Demonstrations Project
- Kumar, Piyush. "A Simple backtracking implementation in C++". http://www.compgeom.com/~piyush/teach/3330/homeworks/knightour.cpp.
- Horsell, Kym. "A Simple implementation in standard Prolog". http://junk.kymhorsell.com/knight.html.
- An implementation in C#
- Knight's Tours Using a Neural Network Program that creates tours using a neural network, plus gallery of images.
- An interactive version in JavaScript
- Knight's Tour in form of jQuery plugin